Legendre-transformasjon

En Legendre-transformasjon er i matematikken en metode for å omskrive en konveks funksjon av en variabel til en ny funksjon av den deriverte av den opprinnelige funksjonen. Den ble funnet i 1787 av den franske matematiker Adrien-Marie Legendre i forbindelse med hans interesse for såkalte minimale flater som han ville beskrive ved hjelp av deres tangentplan.

Definisjon

Den Legendre-transformerte er gitt ved skjæringspunktet g(p) med y-aksen for tangenten med stigningstall p i punktet (x,y) tll den gitte funksjonen y(x).

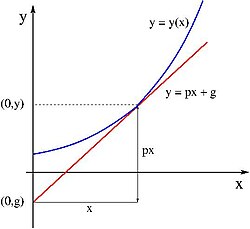
En kontinuerlig funksjon y = y(x) er konveks når dens deriverte er en økende funksjon av den variable x. Det er ekvivalent med å si at den andrederiverte av funksjonen alltid er positiv. Det eksisterer da en entydig sammenheng mellom x og den deriverte p = dy/dx. Dette er en implisitt ligning som gir x = x(p). Man kan nå konstruere en ny og ekvivalent funksjon som har p som argument ved å betrakte den rette linjen som er tangent til y = y(x) i punktet (x,y). Denne linjen skjærer y-aksen i punktet (0,g). For hvert argument x vil den deriverte ha en verdi p som gir en entydig verdi

$g=y-px$

som vist geometrisk i figuren til høyre. Man kan derfor betrakte g = g(p) som en funksjon av p når man benytter at x = x(p). Dette er den Legendre-transformerte funksjonen g(p) er den opprinnelige funksjonen y(x). De to variable x og p sies ofte å være konjugerte med hverandre. Man kan også definere den Legendre-transformerte med motsatt fortegn av hva som er valgt her.

Tar man differensialet av den nye funksjonen g = g(p), finner man dg = dy - pdx - xdp. Men nå er per definisjon dy = pdx slik at dg = - xdp. Derfor har man det viktige resultatet at x = - dg/dp som tilsvarer at p = dy/dx for den konjugerte variable.

Eksempel

Funksjonen y = x² kan benyttes til å gi en enkel illustrasjon av transformasjonen. I dette tilfellet er p = d(x²)/dx = 2x. Sammenhengen mellom x og p blir da ganske enkelt x = p/2. Uttrykt ved den opprinnelige variable, blir den transformerte funksjonen derfor g = x² - 2x⋅x = - x². Dette resultatet kan nå skrives som en funksjon av den konjugerte variable, g(p) = - (p/2)² = - p²/4. Man sjekker nå lett at den Legendre-transformerte av denne funksjonen, er den opprinnelige.

Funksjon av flere variable

Ofte inneholder den gitte funksjonen ekstra variable som ikke inngår direkte i transformasjonen. De sies å være passive. Med en ekstra variabel er da y = y(x,t) hvor t er en passiv variabel. Tangenten i x-retning har nå helningskoeffisient gitt ved den partiellderiverte p = ∂y/∂x som beregnes ved å holde t konstant under derivasjonen. Igjen kan man definere en Legendre-transformert funksjon ved g = y - px. I differensialet dg = dy - pdx - xdp er nå dy = (∂y/∂x)dx + (∂y/∂t)dt slik at man finner

$dg={\Big (}{\partial y \over \partial x}-p{\Big )}dx-xdp+{\partial y \over \partial t}dt$

Her er det første leddet lik null som følge av definisjonen p = ∂y/∂x. Dermed har man at dg = - xdp + (∂y/∂t)dt. Funksjonen g kan derfor betraktes som en funksjon av den nye variable p samt den passive variable t, det vil si at g = g(p,t). Videre ser man at denne nye funksjonen har ∂g/∂p = - x og ∂g/∂t = ∂y/∂t som er viktige relasjoner i praktiske anvendelser. Denne konstruksjonen kan opplagt utvides til å gjelde for funksjoner med flere passive variable.

Eksempel

En enkel funksjon med en passive variabel er y = tx lnx som er konveks når x > 0. Da blir p = ∂y/∂x = t(1 + lnx). Løses denne ligningen med hensyn på x, finner man at x = (1/e)e ^p/t. Dermed blir

$g=f-xp=tx\ln x-xt(1+\ln x)=-xt$

som gir

$g(p,t)=-{t \over e}e^{p/t}$

når man setter inn for x. Dette er den Legendre-transformerte funksjonen. Med dette resultatet kan man nå sjekke at ∂g/∂p = - (1/e)e ^p/t = - x som forventet. Videre er ∂g/∂t = - (1/e)e ^p/t(1 - p/t) = x lnx som er akkurat ∂y/∂t.

Anvendelser

Transformasjonen ble etablert av Legendre for å løse rent matematiske problemer han var konfrontert med. Fremdeles har den mange anvendelser innen ren matematikk. I fysikken blir Legendre-transformasjoner benyttet spesielt innen klassisk mekanikk og termodynamikk.

Termodynamikk

En differensiell økning dU av den indre energien til et system i termisk likevekt som skyldes forandringene dV av dets volum og dS av dets entropi, er forbundet gjennom termodynamikkens andre hovedsetning. Denne kan matematisk skrives som

$dU=-PdV+TdS$

hvor P er trykket som systemet er utsatt for og T er temperaturen det har. Dette er et uttrykk for energiens bevarelse. Man kan derfor betrakte den indre enrgien som en funksjon U = U(S,V) hvor P = - (∂U/∂V)_S  og T = (∂U/∂S)_V . Dette gjør det mulig å gjennomføre to forskjellige Legendre-transformasjoner. Enten kan man erstatte volumet V  med den konjugerte variable som er trykket P, eller man kan erstatte entropien S  med den konjugerte variable som er temperaturen T.

I det første tilfellet får man da H = U + PV  som er entalpien til systemet slik at H = H(S,P)  med V = (∂H/∂P)_S  som følger fra definsjonen av den Legendre-transformerte. Videre er T = (∂H/∂S)_P  da S  er en passiv variabel. Den andre muligheten gir F = U - TS  hvor F = F(T,V)  er Helmholtz fri energi. Da vil S = - (∂F/∂T)_V  og P = - (∂F/∂V)_T  da volumet V  denne gangen er passiv.

Denne frie energien kan man nå Legendre-transformeres videre ved å erstatte V med den konjugerte trykkvariable P. Det gir G = F + PV = H -TS  som er Gibbs fri energi G = G(T,P)  med deriverte V = (∂G/∂P)_T  og S = - (∂G/∂T)_P. Alle disse relasjonene mellom variable og tilsvarende deriverte som følger så direkte fra Legendre-transformasjonen, spiller en viktig rolle i beregninger av praktiske konsekvenser av de termodynamiske lover.

Mekanikk

De mekaniske lovene kan formuleres på to tilsynelatende, forskjellige måter. Hvis man benytter Lagrange-mekanikk, kan de alle utledes fra Lagrange-funksjonen for systemet. Hvis man betrakter bare en dynamisk variabel q som varierer med tiden t, er Lagrange-funksjon L = L(q,q',t) hvor den deriverte q' = dq/dt er en generalisert hastighet. Fra prinsippet om minste virkning følger da bevegelsesligningen

${\partial L \over \partial q}-{d \over dt}\left({\partial L \over \partial q'}\right)=0$

som er en differensialligning av andre orden i tiden. Det siste leddet inneholder p = ∂L/∂q' som er definert som den kanoniske impulsen for systemet. Bevegelsesligningen kan derfor skrives som p' = ∂L/∂q.

Ut fra definisjonen for impulsen ser man at Lagrange-funksjonen kan Legendre-transformeres til en ny funksjon H = pq' - L hvor man erstatter en hastighetsvariabel q'  med en impulsvariabel p = ∂L/∂q' . Den transformerte funksjonen er da H = H(q,p,t) og kalles for Hamilton-funksjonen for systemet. Da q er en passive variabel under denne transformasjonen, vil ∂H/∂q = - ∂L/∂q = - p'  når man passer på at denne Legendre-transformasjonen har motsatt fortegn av hva som ble benyttet over. Av samme grunn vil derfor q' = + ∂H/∂p.

Hamilton-mekanikk er dermed ikke noe annet enn Legendre-transformert Lagrange-mekanikk. I stedet for å ha en andreordens differensialligning å løse, kan man da i stedet benytte de to førsteordens differensialligningene

${dq \over dt}={\partial H \over \partial p}\,,\;\;\;\;\;\;{dp \over dt}=-{\partial H \over \partial q}$

for å beregne bevegelsen. Mange ganger kan dette være enklere selv om fysikken er den samme. Dette er Hamiltons bevegelsesligninger og kan lett generaliseres for systemer med et vilkårlig antall dynamiske variable.

Litteratur

• M.L. Boas, Mathematical Methods in the Physical Sciences, John Wiley & Sons, New York (1983). ISBN 0-471-04409-1.

Eksterne lenker

• MathWorld: Legendre Transformation